Find Each Missing Angle Measure
Missing Angles in Triangles
Missing Angles in Triangles Knowing that a triangle contains 180° makes computing the mensurate of a missing angle much simpler.
Let's have a look at some examples.
Example #1:
Determine the measure of angle x.
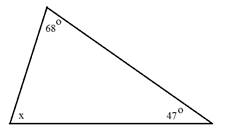
Footstep 1: Add together the known angles.
68° + 47° = 115°
Footstep 2: Decrease the sum from 180°.
180° - 115° = 65°
The measure out of bending ten is 65°.
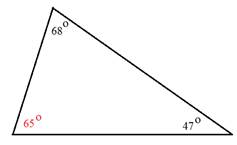
Example #2:
Determine the measure out of bending y.
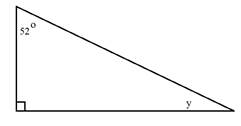
Notice that this triangle has a right bending in the lesser left corner. This angle measures 90°.
Step i: Add the measure out of the given angles together.
52° + ninety° = 142°
Footstep 2: Subtract the sum from 180°.
180° - 142° = 38°
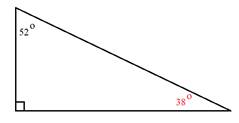
The third angle measures 38°.
Instance iii:
Determine the measure out of angle m.
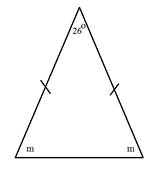
Discover that this triangle is isosceles. That means that not only are 2 of the sides equal but two of the angles are too equal. The solution to this problem will be slightly different than the solution to the others.
Step 1: Subtract the know angle from 180°.
180° - 26° = 154°
Footstep 2: Divide the difference by two to get the measure of each angle.
154° ÷ 2 = 77°
Each angle m measures 77°.
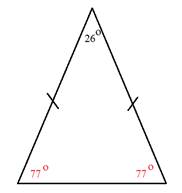
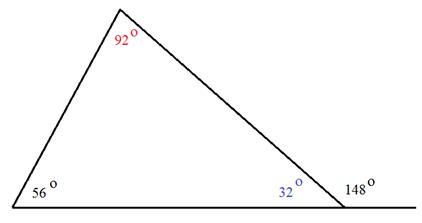
Example 4:
Determine the measure of angle h.
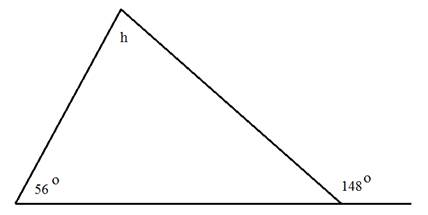
Notice that this triangle gives an angle outside of the triangle. In that location are a couple of unlike ways you can use this information to determine the measure out of angle h.
Hither is one method:
Footstep one: Determine the measure of the angle side by side to 148°.
The two angles make a straight line and therefore have a sum of 180°.
180° - 148° = 32° Step 2: Add together the 2 known angles inside the triangle. 56° + 32° = 88° Pace 3: Subtract the sum from 180°. 180° - 88° = 92° The measure of bending h is 92°. Let'due south Review To determine to measure of the unknown angle, be certain to use the total sum of 180°. If two angles are given, add them together and then subtract from 180°. If two angles are the same and unknown, subtract the known angle from 180° and then dissever by 2. 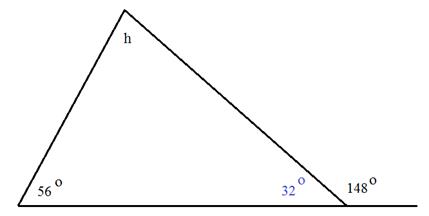
Find Each Missing Angle Measure,
Source: https://www.softschools.com/math/geometry/topics/missing_angles_in_triangles/
Posted by: mccunegonded.blogspot.com


0 Response to "Find Each Missing Angle Measure"
Post a Comment